این مطلب از سایت Code Project مستقیما آورده شده است

 

با تشکر از آقای مهندس آذرنیا که این مقاله را معرفی کردند.

 

Connected Component Labeling Algorithm

Omar Gameel Salem, 2 Feb 2014 CPOL

 

vote 1vote 2vote 3vote 4vote 5

 

Implementation of Connected Component Labeling.

 

• Download source code

Contents

• Overview
  • In five seconds
  • In five minutes
• What to expect
• Code
• How it works
• Step by step walk through
• Tricky part: Merging labels

Overview

In five seconds 

Detection of connected objects in an image, mainly used in image analysis and OCR.

In five minutes

Connected-component labeling (alternatively connected-component analysis, blob extraction, region labeling, blob discovery, or region extraction) is an algorithmic application of graph theory, where subsets of connected components are uniquely labeled based on a given heuristic. Connected-component labeling is not to be confused with segmentation.

Connected-component labeling is used in computer vision to detect connected regions in binary digital images, although color images and data with higher-dimensionality can also be processed.^[1][2] When integrated into an image recognition system or human-computer interaction interface, connected component labeling can operate on a variety of information.^[3][4] Blob extraction is generally performed on the resulting binary image from a thresholding step. Blobs may be counted, filtered, and tracked.

Blob extraction is related to but distinct from blob detection.

What to expect

Input

An image containing two shapes:

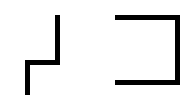
Output

Now each is separated into single images:

Code

 

The Interface IConnectedComponentLabeling holds one function That takes a Bitmap as an input an returns a collection of discovered objects. 

Collapse | Copy Code

public interface IConnectedComponentLabeling
{
    IDictionary<int, Bitmap> Process(Bitmap input);
}

Usage:

Collapse | Copy Code

IConnectedComponentLabeling target = new CCL();
Bitmap input = new Bitmap(AppDomain.CurrentDomain.BaseDirectory + @"\Test.bmp");

var images= target.Process(input);
foreach (var image in images)
{
    image.Value.Save(savePath + image.Key + ".bmp");
}

The implementation class contains the virtual function CheckIsBackGround(), so you can extend the class, and override this method it to suit the background condition of your image:

Collapse | Copy Code

#region Protected Functions

protected virtual bool CheckIsBackGround(Pixel currentPixel)
{
    return currentPixel.color.A == 255 && currentPixel.color.R == 255 && 
             currentPixel.color.G == 255 && currentPixel.color.B == 255;
}

#endregion

How it works

First pass (assigning labels)

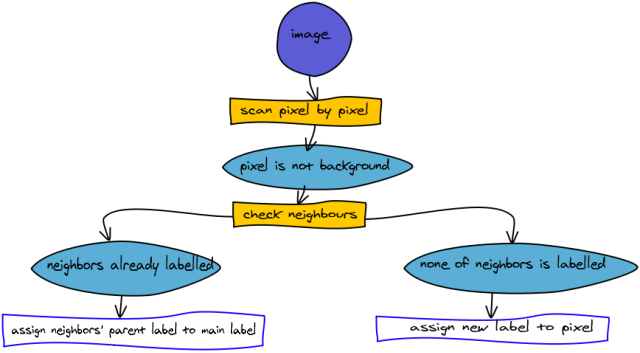
Second pass (aggregation)

Step by step walkthrough

In the beginning, we have this image, we start with currentLabelCount = 1.

We found our non-background pixel:

get its non-background neighbors:

None of the neighbors is labeled yet, we set the current pixel to the currentLabelCount and increment it, we also set the label's parent to itself (we'll get into that in a second):

on to the next pixel, this one has a neighbour which is already labeled:

assigns the pixel's parent label to that of the neighbour:

We continue on, none of the neighbours of this pixel is labeled:

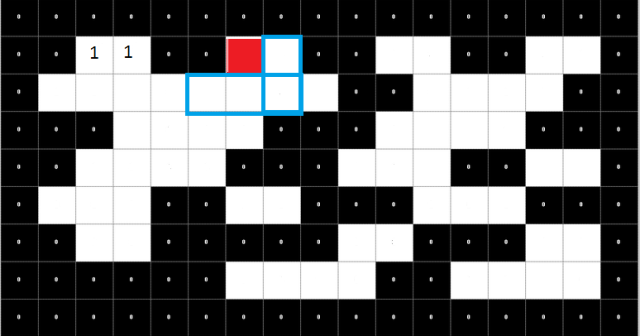
We increment currentLabelCount and assign it to the pixel, again its parent is set to itself: 

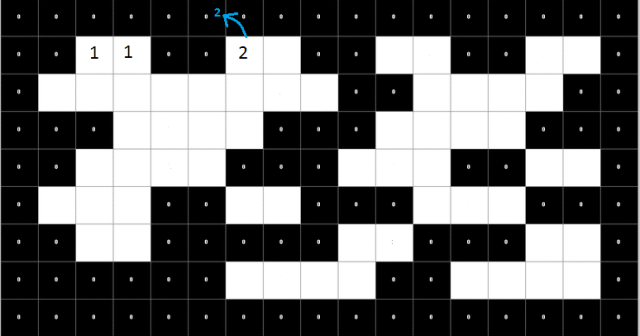
It gets interesting here, when neighbors have different labels:

 

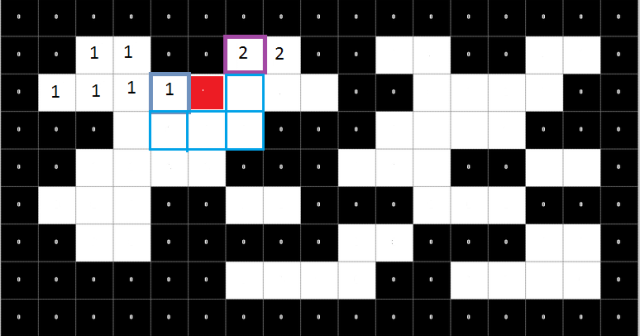
1. We choose main label, i.e.: that would be the smallest label in the discovered list--> (1)
2. We set it to be the parent of the other labels

 

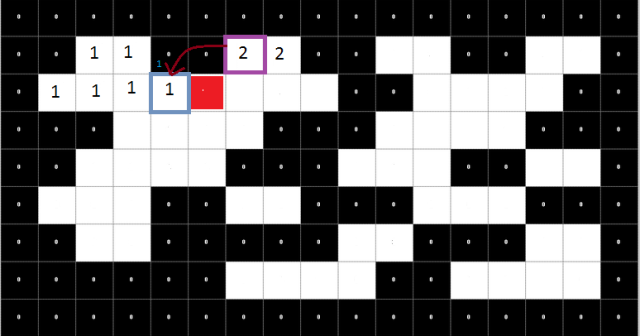
A few more rounds and we should end up with this. Notice the blue number in the upper right corner, that's the parent label, the de facto one upon which we aggregate later.

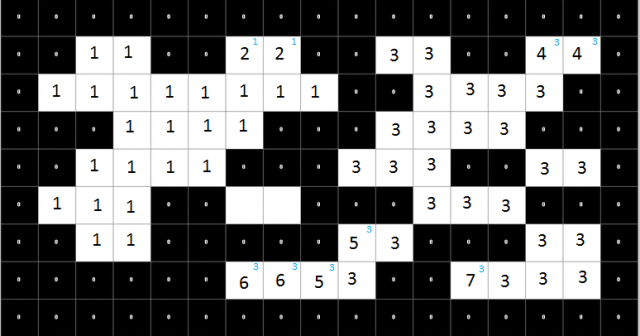
That's it, now all we have to do is pass the image again pixel by pixel, getting the root of each (if labeled) and store it in our patterns' list.

Collapse | Copy Code

private Dictionary<int, List<Pixel>> AggregatePatterns(Dictionary<int, 
          Label> allLabels, int width, int height)
{
    var patterns = new Dictionary<int, List<Pixel>>();

    for (int i = 0; i < height; i++)
    {
        for (int j = 0; j < width; j++)
        {
            int patternNumber = _board[j, i];

            if (patternNumber != 0)
            {
                patternNumber = allLabels[patternNumber].GetRoot().Name;

                if (!patterns.ContainsKey(patternNumber))
                {
                    patterns.Add(patternNumber, new List<Pixel>());
                }

                patterns[patternNumber].Add(new Pixel(new Point(j, i), Color.Black));
            }
        }
    }

    return patterns;
}

Tricky part: Merging labels  

To join labels in a same set, we have the following class (which implements the union find algorithm):

Collapse | Copy Code

using System;
using System.Collections.Generic;
using System.Text;

namespace ConnectedComponentLabeling
{
    internal class Label
    {
        #region Public Properties

        public int Name { get; set; }

        public Label Root { get; set; }

        public int Rank { get; set; }

        #endregion

        #region Constructor

        public Label(int Name)
        {
            this.Name = Name;
            this.Root = this;
            this.Rank = 0;
        }

        #endregion

        #region Public Methods

        internal Label GetRoot()
        {
            if (this.Root != this)
            {
                this.Root = this.Root.GetRoot();//Compact tree
            }

            return this.Root;
        }

        internal void Join(Label root2)
        {
            if (root2.Rank < this.Rank)//is the rank of Root2 less than that of Root1 ?
            {
                root2.Root = this;//yes! then Root1 is the parent of Root2 (since it has the higher rank)
            }
            else //rank of Root2 is greater than or equal to that of Root1
            {
                this.Root = root2;//make Root2 the parent

                if (this.Rank == root2.Rank)//both ranks are equal ?
                {
                    root2.Rank++;//increment Root2, we need to reach a single root for the whole tree
                }
            }
        }

        #endregion
    }
}

Pay special attention to the recursive function GetRoot(), that's how we reach the parent of any label.

Remember this part? This is what the function Join(Label root) does. Now let's say we have three labels, 1, 2, and 3, and we picked 1 to be our current label; all we have to do is loop the other labels, if their roots don't match, set their root to that of the label we just picked.  

Conclusion

Hope I delivered a clear explanation, feel free to comment or ask . Drawings by zwibbler

 

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)

Share

• email

About the Author

Omar Gameel Salem

Software Developer
Australia

Enthusiastic programmer/researcher, passionate to learn new technologies, interested in problem solving, data structures, algorithms AI, machine learning and nlp.
 
Amateur guitarist/ keyboardist, squash player.
 
If you have a question\suggestion about one of my articles, or you want an algorithm implemented in C#, feel free to contact me.